解方程计算器电脑版

解方程计算器是一款用户友好的工具，旨在帮助用户快速而准确地求解方程中的X值。它支持一元一次方程和二元一次方程的计算，非常简单实用。用户只需输入完整的方程，便能迅速得到所需的X值。此外，该软件占用内存少，无需担心电脑性能问题，同时能够确保返回的X值数据准确可靠。不论是学术研究还是日常使用，解方程计算器都是理想的选择。欢迎有需要的用户下载体验！

软件特色

1、支持一元一次方程和二元一次方程计算

2、使用简单，只需要输入一个完整的方程式，即可得出相应的X值

3、功能强大，占用内存极少，但可帮助用户快速得出一个准确无误的X值

4、绿色免安装，无需繁琐的安装教程，点击即可使用

5、数据准确无误，得到的数据保证精确

6、无任何广告，采用VB开发，只有计算按键，其他无任何广告界面

使用教程

1、程序免安装，用户仅需双击解方程计算器.exe即可打开程序

2、选择需要解的方程类型，程序支持一元一次方程和二元一次方程的计算

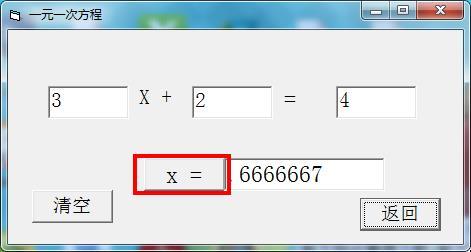
3、进入算法界面，输入相应的解方程数据，完成点击X=按键即可获得相应的X值

方程与等式的关系

方程一定是等式，但等式不一定是方程

例子：a+b=13 符合等式，有未知数。这个是等式，也是方程

1+1=2 ，100×100=10000。这两个式子符合等式，但没有未知数，所以都不是方程

在定义中，方程一定是等式，但是等式可以有其他的，比如上面举的1+1=2，100×100=10000，都是等式，显然等式的范围大一点

解方程依据

一、移项变号：把方程中的某些项带着前面的符号从方程的一边移到另一边，并且加变减，减变加，乘变除以，除以变乘

二、等式的基本性质

1.性质1

等式两边同时加(或减)同一个数或同一个代数式，所得的结果仍是等式。用字母表示为：若a=b，c为一个数或一个代数式。则：(1)  (2) 

2.性质2

等式的两边同时乘或除以同一个不为0的数,所得的结果仍是等式

用字母表示为：若a=b，c为一个数或一个代数式（不为0）。则：

a×c=b×c 或 

3.性质3

若a=b,则b=a（等式的对称性）

4.性质4

若a=b,b=c则a=c（等式的传递性）

解方程步骤

方法一：1.能计算的先计算； 2.转化——计算——结果

方法二：从前往后算，算到只剩一个数时便可直接计算。

【相关概念

方程式或简称方程，是含有未知数的等式。即：⒈方程中一定有含一个或一个以上未知数的代数式；2.方程式是等式，但等式不一定是方程。

未知数：通常设x.y.z为未知数，也可以设别的字母，全部小写字母都可以。

次：方程中次的概念和整式的次的概念相似。指的是含有未知数的项中，未知数次数最高的项。而次数最高的项，就是方程的次数

解：方程的解，指使，方程的根是方程两边相等的未知数的值，指一元方程的解，两者通常可以通用

解方程：求出方程的解的过程，也可以说是求方程中未知数的值的过程，或说明方程无解的过程叫解方程

方程中，恒等式叫做恒等方程，矛盾式叫做矛盾方程。在未知数等于某特定值时，恰能使等号两边的值相等者称为条件方程，例如 ，在 时等号成立,使方程左右两边相等的未知数的值叫做方程的解

同解方程：

如果两个方程的解相同，那么这两个方程叫做同解方程

方程的同解原理：

1.方程的两边都加或减同一个数或同一个等式所得的方程与原方程是同解方程

2.方程的两边同乘或同除同一个不为0的数所得的方程与原方程是同解方程

整式方程：方程的两边都是关于未知数的整式的方程叫做整式方程

分式方程：分母中含有未知数的方程叫做分式方程

一元一次方程解法

只含有一个未知数，且未知数次数是一的整式方程叫一元一次方程。通常形式是ax+b=0(a，b为常数，且a≠0）

一般解法

1.去分母 方程两边同时乘各分母的最小公倍数。

2.去括号 一般先去小括号，再去中括号，最后去大括号。但顺序有时可依据情况而定使计算简便。可根据乘法分配律。

3.移项 把方程中含有未知数的项移到方程的另一边，其余各项移到方程的另一边移项时别忘记了要变号。(一般都是这样：（比方）从 5x=4x+8 得到 5x - 4x=8 ；把未知数移到一起！

4.合并同类项 将原方程化为ax=b(a≠0)的形式。

5.化系数为一 方程两边同时除以未知数的系数。

6.得出方程的解。

例如：

3x=5×6

解:3x=30

x=30÷3

x=10

（注:解方程时最好把等号对齐）

二元一次方程解法

一、定义

1.二元一次方程定义：一个含有两个未知数，并且未知数的次数都是1的整式方程，叫二元一次方程

2.二元一次方程组定义：由两个二元一次方程组成的方程组，叫二元一次方程组

3.二元一次方程的解：使二元一次方程两边的值相等的两个未知数的值，叫做二元一次方程的解

4.二元一次方程组的解：二元一次方程组的两个公共解，叫做二元一次方程组的解

二、一般解法

消元：将方程组中的未知数个数由多化少，逐一解决

消元的方法有两种:

1.代入消元

例：解方程组x+y=5① 6x+13y=89②

解：由①得x=5-y③ 把③带入②，得6(5-y)+13y=89，解得y=59/7

把y=59/7带入③，得x=5-59/7，即x=-24/7

∴x=-24/7，y=59/7

这种解法就是代入消元法

2.加减消元

例：解方程组x+y=9① x-y=5②

解：①+②，得2x=14，即x=7

把x=7带入①，得7+y=9，解得y=2

∴x=7，y=2

这种解法就是加减消元法

二元一次方程组的解有三种情况：

1.有一组解

如方程组x+y=5① 6x+13y=89②的解为x=-24/7，y=59/7。

2.有无数组解

如方程组x+y=6① 2x+2y=12②，因为这两个方程实际上是一个方程（亦称作方程有两个相等的实数根），所以此类方程组有无数组解。

3.无解

如方程组x+y=4① 2x+2y=10②，因为方程②化简后为x+y=5，这与方程①相矛盾，所以此类方程组无解